Functions: Power functions and root functions
 Root function
Root function
Root function
The simplest root function is the function \[f(x)=\sqrt{x}\]
The table with this root function is (all roots rounded to 2 decimals):
#\begin{array}{c|c|c|c|c|c|c|c}
x & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\
\hline y & 0 & 1 & 1.41 & 1.73 & 2 & 2.24 & 2.45
\end{array}#
The graph of the function is half a parabola with origin #\rv{0,0}#.
Since the root is only defined for non-negative numbers, the domain of the root function is equal to the interval #\ivco{0}{\infty}#.
Since the root of a non-negative number is a non-negative number in itself, the range is also equal to the interval #\ivco{0}{\infty}#.
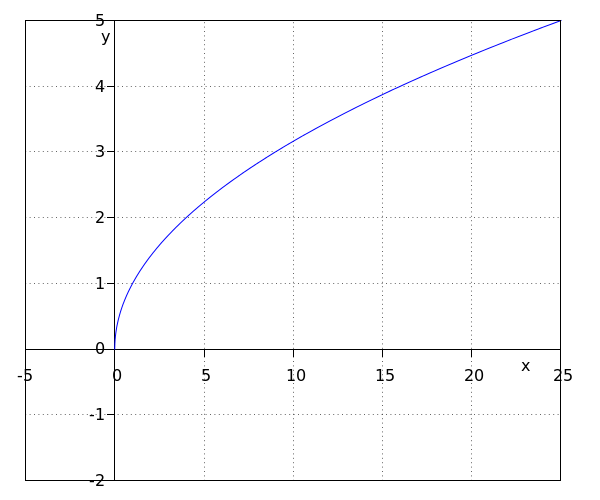
Take a look at the function #f(x)=\sqrt{x}#. Does the point #\rv{10, 3.16}# lie on the graph on this function?
In here, you can round the #y#-value of the point to #2# decimals, if needed.
In here, you can round the #y#-value of the point to #2# decimals, if needed.
Yes
We substitute #x=10# in the formula. This is done in the following way:
\[f(10)=\sqrt{10}=3.16\]
Hence, #\rv{10, 3.16}# is a point on the graph.
We substitute #x=10# in the formula. This is done in the following way:
\[f(10)=\sqrt{10}=3.16\]
Hence, #\rv{10, 3.16}# is a point on the graph.
Unlock full access


Teacher access
Request a demo account. We will help you get started with our digital learning environment.
Student access
Is your university not a partner?
Get access to our courses via Pass Your Math independent of your university. See pricing and more.
Or visit omptest.org if jou are taking an OMPT exam.
Or visit omptest.org if jou are taking an OMPT exam.



