Quadratic inequalities

Quadratic equations: Quadratic inequalities

Quadratic inequalities

Just as with linear inequalities, we can create an inequality with quadratics. We will first take a look at how to solve a quadratic inequality.

We solve the inequality #\blue{2x^2+4x+3} \gt \green{-x^2-2x+6}#.

Step 1

We first solve the equality #\blue{2x^2+4x+3} = \green{-x^2-2x+6}#. Therefore we first reduce the equality to #0#.

\[\begin{array}{rcl}2x^2+4x+3&=&-x^2-2x+6 \\ &&\phantom{xx}\blue{\text{the equation to solve}}\\ 3x^2+6x-3 &=&0 \\ &&\phantom{xx}\blue{\text{reduce to }0} \end{array}\]

Next we apply the quadratic formula. Therefore we define the letters #a#, #b# and #c#.

\[a=3, b=6 \text{ and } c=-3\]

Next, we calculate the discriminant.

\[D=6^2-4 \cdot 3 \cdot -3 =72\]

After that, we determine the solutions

\[x=\frac{-6-\sqrt{72}}{2\cdot 3} \lor x=\frac{-6+\sqrt{72}}{2\cdot 3} \]

Which we simplify to:

\[x=-1- \sqrt{2} \lor x=-1+ \sqrt{2} \]

Step 2

We create the graphs of #y=\blue{2x^2+4x+3}# and #y=\green{-x^2-2x+6}\ (dashed)#. The intersection points are drawn in orange.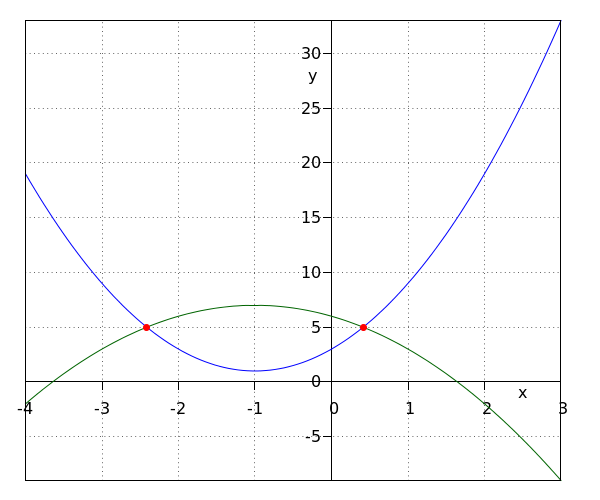

Step 3

We will determine the solution by means of step 1 and 2.

On the left of #x=-1-\sqrt{2}# and on the right of #x=-1+\sqrt{2}# the graph of #y=\blue{2x^2+4x+3}# lies above the graph of #y=\green{-x^2-2x+6}#.

hence, the solution is #x \lt -1-\sqrt{2} \lor x \gt -1+\sqrt{2}#.

In general, we can apply the following procedure.

Solving a quadratic inequality

	Procedure
	We solve the inequality #\blue{a_1 x^2+b_1x+c_1} \gt \green{a_2x^2+b_2x+c_2}\ (dashed)#, in which #a_1 \ne 0#.
Step 1	We first solve the equality \[\blue{a_1 x^2+b_1x+c_1} = \green{a_2x^2+b_2x+c_2}\]
Step 2	We draw the graphs #y=\blue{a_1 x^2+b_1x+c_1}# and #y=\green{a_2x^2+b_2x+c_2}#.
Step 3	With help of step 1 and 2, determine for which value of #x# the inequality holds. In the coordinate system, the bigger graph is the one that lies above the other.

Note that this procedure also holds for the inequality signs #\geq#, but the #x#-values of the intersection points are also part of the solution.

All or none

If there are no intersection points found in step 1, then there are two options with regard to the solution of the inequality.

1) all points of #x# are a solution of the inequality. The inequality is always true.

2) no points of #x# are a solution of the inequality. The inequality is never true.

The same holds if we have found an intersection point in step 1, but that being a point of tangency. Then the parabolas are equal in that point and at all other points, the inequality is true or not.

Example

The quadratic formulas #y=\blue{x^2+5x+3}# and #y=\green{-x^2-5x-\frac{19}{2}}#.

The intersection point of the two formulas is #\rv{-\frac{5}{2}, -\frac{7}{2}}#.

The inequality #\blue{x^2+5x+3} \geq \green{-x^2-5x-\frac{19}{2}}# is true for all points of #x#.

The inequality #\blue{x^2+5x+3} \lt \green{-x^2-5x-\frac{19}{2}}# is not true for any point of #x#.

Solve #a# in the inequality
\[-2\cdot a^2+15\cdot a+7 \lt 3\cdot a^2+12\cdot a+4\tiny\]
Give your answer in the form

#a \gt a_1\land a \lt a_2# or #a\lt a_1 \lor a \gt a_2#;
#a \lt a_1# or #a \gt a_1#;
#none# or #all#,

in which #a_1# and #a_2# are numbers.

#a\lt {{3-\sqrt{69}}\over{10}}\lor a\gt {{\sqrt{69}+3}\over{10}}#

Step 1	We solve the equality #-2\cdot a^2+15\cdot a+7=3\cdot a^2+12\cdot a+4#. This is done in the following way: \[\begin{array}{rcl} -2\cdot a^2+15\cdot a+7 &=& 3\cdot a^2+12\cdot a+4\\ &&\phantom{xxx}\blue{\text{the original equality}}\\ -5\cdot a^2+3\cdot a+3&=&0\\ &&\phantom{xxx}\blue{\text{all terms moved to the left hand side}}\\ \text{discr‍iminant } &=& b^2-4ac \\ &&\phantom{xxx}\blue{\text{formula discrim‍inant}}\\ &=& 3^2 - 4 \cdot \left(-5\right) \cdot 3 \\&&\phantom{xxx}\blue{\text{formula entered}}\\ &=& 69\\&&\phantom{xxx}\blue{\text{calculated}}\\ \text{number of solutions } &=& 2\\&&\phantom{xxx}\blue{\text{since discrimant bigger than }0}\\ a=\dfrac{-b-\sqrt{D}}{2 \cdot a} &\lor& a=\dfrac{-b+\sqrt{D}}{2 \cdot a} \\&&\phantom{xxx}\blue{\text{formula solutions}}\\ a=\dfrac{-3 - \sqrt{69}}{2 \cdot \left(-5\right)} &\lor& a=\dfrac{-3 + \sqrt{69}}{2 \cdot \left(-5\right)} \\&&\phantom{xxx}\blue{\text{formula entered}}\\ \displaystyle a= {{\sqrt{69}+3}\over{10}} &\lor& \displaystyle a = {{3-\sqrt{69}}\over{10}} \\&&\phantom{xxx}\blue{\text{calculated}}\\ \end{array}\]
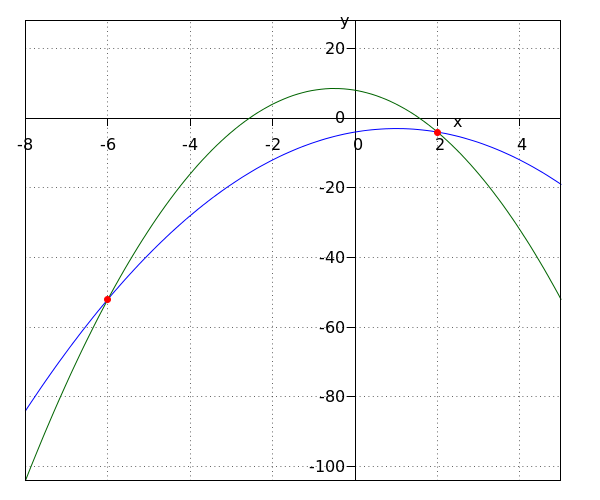
Step 2	We sketch the graphs of #y=-2\cdot a^2+15\cdot a+7# (blue solid) and #y=3\cdot a^2+12\cdot a+4# (green dashed).
Step 3	We can now read the answer of the inequality. \[a\lt {{3-\sqrt{69}}\over{10}}\lor a\gt {{\sqrt{69}+3}\over{10}}\]

New example