Fonctions réciproques

Fonctions: Fonctions puissances et fonctions irrationnelles

Fonctions réciproques

Nous considérons les fonctions #\blue{f(x)}=\blue{x^2}# et #\green{g(x)}=\green{\sqrt{x}}# sur le domaine #\ivco{0}{\infty}#.

Pour ces fonctions, nous avons #\blue f(\green{g(x)})=\left(\green{\sqrt{x}}\right)^\blue2=x# pour tous #x# appartenant à #\ivco{0}{\infty}#.

Ainsi, #\green{g(x)}# est appelée réciproque de #\blue{f(x)}#.

De même, nous avons #\green g(\blue{f(x)})=\green{\sqrt{\blue{x^2}}}=x# pour tous #x# appartenant à #\ivco{0}{\infty}#.

Ainsi, #\blue{f(x)}# est appelée réciproque de #\green{g(x)}#.

Réciproque

La fonction #\blue{f(x)}# admet comme fonction réciproque #\green{g(x)}# si \[\blue f(\green{g(x)})=x\]

Du point de vue géométrique, le graphe de la réciproque de #\green{g(x)}# est le symétrique du graphe de #\blue{f(x)}# par rapport à la droite #y=x#.

Nous pouvons également noter la réciproque de #f(x)# par #f^{-1}(x)#.

En déterminant la réciproque d'une fonction, le domaine de cette fonction est important. Le domaine de
#\blue{f(x)}# est l'ensemble image de #\green{g(x)}# et le domaine de #\green{g(x)}# est l'ensemble d'image de #\blue{f(x)}#. Alors, la réciproque de la fonction #\green{g(x)}# est définie sur l'ensemble d'image de la fonction #\blue{f(x)}#.

Exemple
Dans l'image #\blue{f(x)}=\blue{(x+1)^2}# sur le domaine #x \ge -1# et son réciproque #\green{g(x)}=\green {\sqrt{x}-1}# sur le domaine #x \ge 0#

Domaine

Le domaine de la fonction #\blue{f(x)}=\blue{(x+1)^2}# se compose de tous les nombres et l'ensemble d'image se compose de tous les nombres non négatifs. Sa fonction réciproque #\green{g(x)}=\green{\sqrt{x}-1}# a comme domaine les nombres non négatifs, et comme l'emsemble d'image aussi les nombres non négatifs. Donc la fonction #\blue{f(x)}=\blue{(x+1)^2}# admet une réciproque que sur le domaine des nombres non négatifs.

Inversement, nous avons que la fonction #\green{g(x)}=\green{\sqrt{x}-1}# a la fonction #\blue{f(x)}=\blue{(x+1)^2}# comme réciproque, mais seulement sur le domaine de tous les nombres plus grand ou égal à #-1# car c'est l'ensamble d'image de la fonction #\green{g(x)}# et alors le domaine de #\blue{f(x)}#.

Dans la suite, nous ne mentionnerons pas les limitations du domaine d'une fonction réciproque. Nous les supposons de manière implicite.

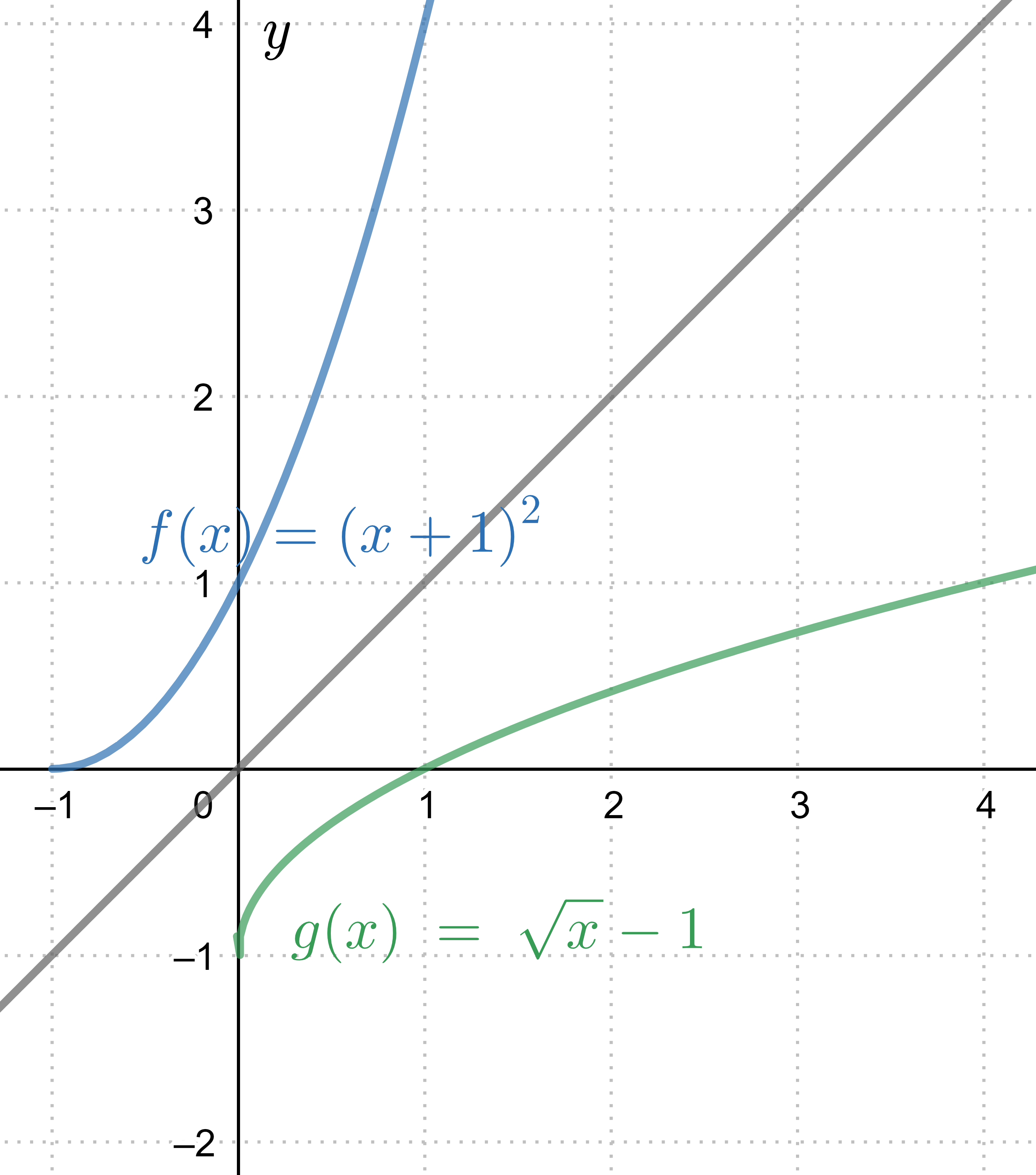
Détermination de la fonction réciproque

	Procédure Nous déterminons la fonction réciproque #\green{f^{-1}(x)}# de la fonction #\blue{f(x)}#.	Exemple #\blue{f(x)}=\left(x-4\right)^2#.
Étape 1	Écrivez la fonction comme une équation, c.-à-d. sous la forme #y=\ldots#.	#y=\left(x-4\right)^2#
Étape 2	Isolez la variable #x# dans l'équation #y=\ldots#. Cela signifie que l'équation est écrite sous la forme #x=\ldots#.	#x=\sqrt{y}+4#
Étape 3	Échangez dans l'équation, le #y# en #x# et #x# en #y#.	#y=\sqrt{x}+4#
Étape 4	Remplacez #y# par #\green{f^{-1}(x)}#.	#\green{f^{-1}(x)}=\sqrt{x}+4#

Étape 2

Nous passons à l'étape 2 de l'exemple. Nous voulons isoler la variable #x# dans l'équation #y=\left(x-4\right)^2#. Cela se fait par réduction.

\[\begin{array}{rcl}y&=&\left(x-4\right)^2 \\ &&\phantom{xxx}\blue{\text{équation de départ}} \\ \sqrt{y}&=&x-4 \\ &&\phantom{xxx}\blue{\text{application de la racine }} \\ \sqrt{y}+4&=&x \\ &&\phantom{xxx}\blue{\text{addition de }4}\end{array}\]

Donc #x=\sqrt{y}+4#.

Isoler une variable

Notez que isoler une variable est la même chose que déterminer la fonction réciproque.

Nous ne devons plus passer à l'étape 3 et 4, mais nous avons déjà atteint notre objectif à l'étape 2 de la procédure.

Extraire de la racine

À l'étape 2, nous avons extrait la racine carrée des deux côtés pour pouvoir isoler #x# du carré. Nous prenons la racine positive. Comme nous l'avons vu dans l'introduction de la fonction racine carrée, la racine d'un nombre non négatif est un nombre non négatif.

Si un certain domaine est spécifié pour trouver la réciproque, il pourrait être nécessaire de prendre la racine négative.

Isolez #x# dans
\[y=\sqrt{2\cdot x-5}\]
Donnez votre réponse sous la forme #x = ...#

#x={{y^2+5}\over{2}}#

#\begin{array}{rcl}
y&=&\sqrt{2\cdot x-5} \\ &&\phantom{xxx}\blue{\text{équation de départ}}\\
y^2&=& 2\cdot x-5 \\ &&\phantom{xxx}\blue{\text{élévation au carré}}\\
y^2+5&=&2\cdot x \\ &&\phantom{xxx}\blue{\text{soustraction de }-5}\\
{{y^2+5}\over{2}} &=&x \\ &&\phantom{xxx}\blue{\text{division par }2}\\
x&=&{{y^2+5}\over{2}} \\ &&\phantom{xxx}\blue{\text{échange des deux membres }}\\
\end{array}#

Nouveau exemple