Fonctions: Fonctions puissances
 Fonctions puissances
Fonctions puissances
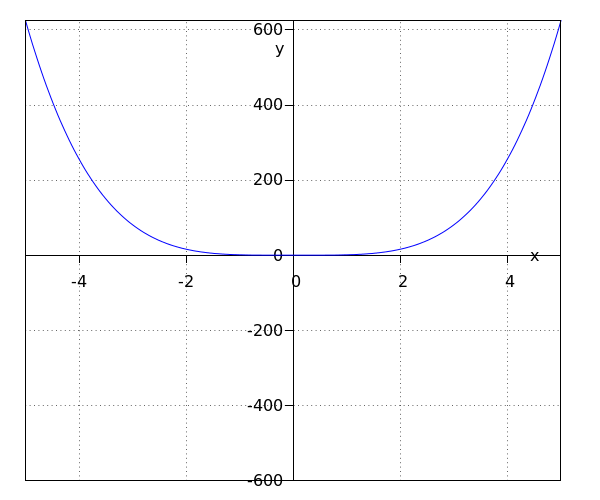
La fonction #\blue {f}# a pour ensemble image #\ivco{0}{\infty}#.
L'axe des #y# est l'axe de symétrie.
Le sommet est #\rv{0,0}#.
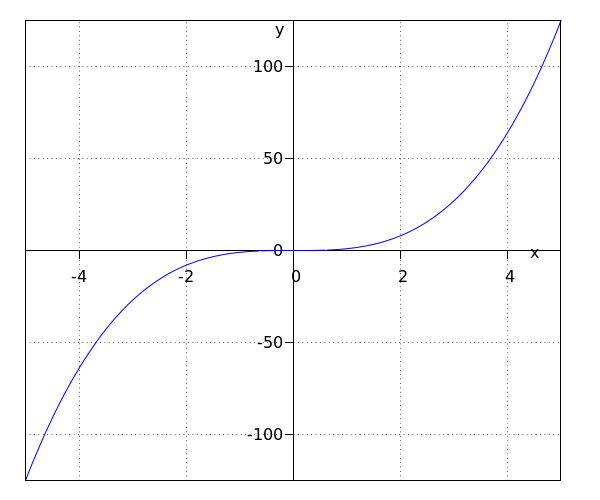
La fonction #\green{g}# a pour ensemble image #\ivoo{-\infty}{\infty}#.
Le point #\rv{0,0}# est le centre de symétrie.
Les deux fonctions de l'exemple ci-dessus sont des fonctions puissances. Leurs graphes diffèrent beaucoup. Cela a avoir avec le fait que #\blue{f}# est une fonction puissance à exposant pair et que #\green g# est fonction puissance à exposant impair.
Une fonction de la forme \[f(x)=\blue{a}x^{\orange{n}}\] avec #\blue{a} \ne 0# est une fonction puissance.
Le graphe d'une fonction puissance à exposant entier #\orange{n} \gt 0# passe par les points #\rv{0,0}# et #\rv{1,\blue a}#.
De plus, les graphes des fonctions puissances diffèrent selon la parité de #\orange{n}#. Si #\orange{n}# est pair, alors le graphe est symétrique par rapport à l'axe des #y#. Si #\orange{n}# est impair, alors le graphe est symétrique par rapport au point #\rv{0,0}#.

Que pouvez-vous dire des valeurs de #n# et #a#?
La valeur de #a# est: positive
Le graphe est symétrique par rapport au point #\rv{0,0}#, donc la valeur de #n# est impaire.
Les ordonnées #y# sont positives pour des abscisses #x# positives, donc la valeur de #a# est positive.

Ou visitez omptest.org si jou prenez un examen de OMPT.



